Answer:
The rate of the boat in still water is 44 mph and the rate of the current is 4 mph
Step-by-step explanation:
x = the rate of the boat in still water
y = the rate of the current.
Distance travelled = 120 mi
Time taken upstream = 3 hr
Time taken downstream = 2.5 hr
Speed = Distance / Time
Speed upstream
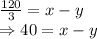
Speed downstream
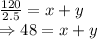
Adding both the equations

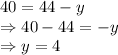
The rate of the boat in still water is 44 mph and the rate of the current is 4 mph