Question

A set of Christmas tree lights consists of 60 identical bulbs connected in series. When they are connected to a constant 240 V electricity supply, the bulbs dissipate 2.00 W of electrical power each. In an attempt to improve performance, an amateur electrician decides to remove 10 bulbs and replace them with connections of effectively zero resistance. Assuming that the bulbs do not burn out, how much power is dissipated by the total set of bulbs when the modified set is switched on?

Answer 1

2.4 watt

Step-by-step explanation:

Case 1 :

n = Number of bulbs = 60

V = Voltage of the source = 240 volts

P = Power dissipated by the bulbs = 2 W

R = Resistance of each bulb

R' = Resistance of the combination of the bulbs = 60 R

Power dissipated is given as

`P = (V^(2))/(R')`

`2 = (240^(2))/((60R))`

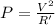
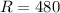`R = 480` ohm

After 10 bulbs are removed

Case 2 :

n' = Number of bulbs in series = 50

V = Voltage of the source = 240 volts

P = Power dissipated by the bulbs = ?

R = Resistance of each bulb = 480 ohm

R' = Resistance of the combination of the bulbs = 50 R = (50) (480) = 24000 ohm

Power dissipated is given as

`P = (V^(2))/(R')`

`P = (240^(2))/(24000)`

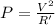
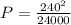
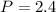`P = 2.4` Watt