Answer:
electric potential is 3.31 ×
 V
V
potential energy is 152 MeV
Step-by-step explanation:
given data
fragment charge Q = 46 protons = 46 × 1.6 ×
 C
C
to find out
electric potential and potential energy
solution
we know here distance from fragment d = 2 ×
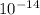 m
m
and constant for electric force k that is 9 ×
 N-m²/C²
N-m²/C²
so that we can find electric potential = kQ/d
electric potential = 9 ×
![10^(9)[/tex ×46 × 1.6 × [tex]10^(-19)](https://img.qammunity.org/2020/formulas/physics/college/mbsqlq0ch38vo6tenmg6g7t04063eajbh8.png) / ( 2 ×
/ ( 2 ×
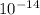 )
)
electric potential = 3.31 ×
 V
V
and
we know relation between electric potential and potential
that is V = U/q
so U will be = qV
now put all value
we get potential energy U
potential energy = 46 × 3.31 ×

potential energy = 1.52 ×
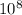 eV
eV
so potential energy = 152 MeV