Question

The time to failure for a gasket follows the Weibull distribution with ß = 2.0 and a characteristic life of 300 days. What is the reliability at 200 days? Also, at how many days does the reliability fall to 95% and 90% reliability?

Answer 1

64.11% for 200 days.

t=67.74 days for R=95%.

t=97.2 days for R=90%.

Step-by-step explanation:

Given that

β=2

Characteristics life(scale parameter α)=300 days

We know that Reliability function for Weibull distribution is given as follows

`R(t)=e^{-\left((t)/(\alpha)\right)^\beta}`

Given that t= 200 days

`R(200)=e^{-\left((200)/(300)\right)^2}`

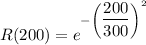
R(200)=0.6411

So the reliability at 200 days 64.11%.

When R=95 %

`0.95=e^{-\left((t)/(300)\right)^2}`

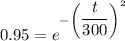
by solving above equation t=67.74 days

When R=90 %

`0.90=e^{-\left((t)/(300)\right)^2}`

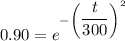
by solving above equation t=97.2 days