Answer:
64.11% for 200 days.
t=67.74 days for R=95%.
t=97.2 days for R=90%.
Step-by-step explanation:
Given that
β=2
Characteristics life(scale parameter α)=300 days
We know that Reliability function for Weibull distribution is given as follows
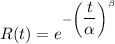
Given that t= 200 days
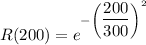
R(200)=0.6411
So the reliability at 200 days 64.11%.
When R=95 %
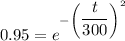
by solving above equation t=67.74 days
When R=90 %
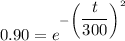
by solving above equation t=97.2 days