Question

You are interested in investing in a five-year bond that pays a 6.6 percent coupon rate with interest to be received semiannually. Your required rate of return is 9.8 percent. What is the most you would be willing to pay for this bond?

Answer 1

Assuming a par value of $1,000, the most i would be willing to pay for this bond is $875.85

Step-by-step explanation:

The price of a bond is equivalent to the present value of all the cash flows that are likely to accrue to an investor once the bond is bought. These cash-flows are the periodic coupon payments that are to be paid semi-annually and the par value of the bond that will be paid at the end of 5 years.

During the 5 years, there are 10 equal periodic coupon payments that will be made. Assuming a par value equal to $1,000, in each year, the total coupon paid will be
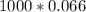`1000*0.066` =$66. This annual payment will be split into two equal payments equal to
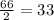`(66)/(2)=33` . This stream of cash-flows is an ordinary annuity.

the required rate of return is to 9.8% per annum which equates to 4.9% per semi annual period.

The PV of the cash-flows = PV of the coupon payments + PV of the par value of the bond

=33*PV Annuity Factor for 10 periods at 4.9%+ $1,000* PV Interest factor with i=4.9% and n =10

`= 33*([1-(1+0.049)^-^1^0])/(0.049)+ (1,000)/((1+0.049)^1^0) =875.85`