Answer:
Assuming a par value of $1,000, the most i would be willing to pay for this bond is $875.85
Step-by-step explanation:
The price of a bond is equivalent to the present value of all the cash flows that are likely to accrue to an investor once the bond is bought. These cash-flows are the periodic coupon payments that are to be paid semi-annually and the par value of the bond that will be paid at the end of 5 years.
During the 5 years, there are 10 equal periodic coupon payments that will be made. Assuming a par value equal to $1,000, in each year, the total coupon paid will be
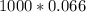 =$66. This annual payment will be split into two equal payments equal to
=$66. This annual payment will be split into two equal payments equal to
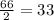 . This stream of cash-flows is an ordinary annuity.
. This stream of cash-flows is an ordinary annuity.
the required rate of return is to 9.8% per annum which equates to 4.9% per semi annual period.
The PV of the cash-flows = PV of the coupon payments + PV of the par value of the bond
=33*PV Annuity Factor for 10 periods at 4.9%+ $1,000* PV Interest factor with i=4.9% and n =10
![= 33*([1-(1+0.049)^-^1^0])/(0.049)+ (1,000)/((1+0.049)^1^0) =875.85](https://img.qammunity.org/2020/formulas/business/college/g3uijowklo3bma5z98k3xj0rh9n5fgrqlz.png)