Question

John hit a golf ball from the ground and it followed the projectile h(t)=-16t²+100t+0, where is the time in seconds, and ℎ is the height of the ball. Use the quadratic formula to solve the two roots. These represent the 2 times that the ball is on the ground. At what time does the golf ball land? What is the max height of the golf ball? At what time (t) is the golf ball at the maximum height?

Answer 1

The maximum height of the golf ball h(t) = 156.25m

The maximum height of the golf ball at t = 3.125 seconds

Explanation:

Step(i):-

Given

h(t)=-16t²+100t ...(i)

Differentiating equation (i) with respective to 't'

`(dh)/(dt) = -16(2t) + 100 (1)`

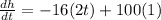
-32t + 100 =0

⇒ -32 t = -100

`t = (100)/(32) = (25)/(8) = 3.125`

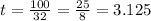
t = 3.125 > 0

Step(ii):-

Given h(t) = -16t²+100t = 0

t ( -16 t + 100 ) =0

t =0 and -16t = -100

t =0 and t = 6.25

Step(iii):-

h(t) = -16t²+100t ...(i)

put t=0 in equation (i)

h(0) = 0

put t = 3.125 in equation (i)

h(t) = -16(3.125)²+100(3.125)

h (t) = 156.25

Put t = 6.25

h(t) = -16(6.25)²+100(6.25)

= 0

The maximum value h(t) = 156.25 at 3.125

final answer:-

The maximum height of the golf ball h(t) = 156.25m

The maximum height of the golf ball at t = 3.125 seconds