Answer:
The probability is 0.0145.
Explanation:
We first calculate two probabilities:
- the probability that a faulty chip is coming from Japan, denoted by P(D∪J), and
- the probability that a faulty chip is coming from the US, denoted by P(D∪A).
And then we sum them up.
Given that the probability of finding a defective chip is conditioned by the probabilities of the chips come from, we deduce that we'll have to use the formulae for extraction without replacement:
P(D∪J) = P(J)*P(D/J)
P(D∪A) = P(A)*P(D/A)
We know that
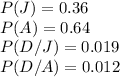
So we can simply calculate
P(D∪J)+P(D∪A) =
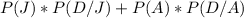
P(D∪J)+P(D∪A) =
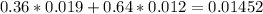
Therefore the rounded answer to 4 decimals would be 0.0145.