Question

Find the domain for the rational function f of x equals quantity x plus 1 end quantity divided by quantity x minus 2 end quantity.

(−∞, 2) (2, ∞)
(−∞, −2) (−2, ∞)
(−∞, 1) (1, ∞)
(−∞, −1) (−1, ∞)

Answer 1

(−∞, 2)∪(2, ∞)

Explanation:

Domain is all the values that "x" can be

since finding all the values which "x" can be is too hard we will find out the values which "x" can't be- this means equating the denominator to "0" so that the function will be undetermined:

`f(x)=(x+1)/(x-2)`

since we need the denominator to be "0" we must use the opposite of (-2) which is "2" so we will substitute "2" in the place of "x"
`f(2)=(2+1)/(2-2)`- the function is now "undetermined" since nothing can be divided by 0 we need to write our answer in proper domain/range format

-Hope this helps!

Answer 2

Option 1.

Explanation:

If a rational function is defined as
`R(x)=(p(x))/(q(x))`, then the domain of the rational function is the intersection of domains of p(x) and q(x) except those values for which q(x)=0.

The given rational function is

`f(x)=(x+1)/(x-2)`

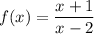
We need find the domain of the given function.

Here, the numerator and denominator both functions are polynomial and domain of a polynomial function is all real number.

So, domain of the given function is all real number except those values of x for which x-2=0.

`x-2=0`

`x=2`

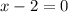
Domain of f(x) = All real numbers except 2.

Domain of f(x) = (−∞, 2)∪(2, ∞)

Therefore, the correct option is 1.