Answer:
The horizontal displacement is 11 units, the vertical displacement is 9 units, and the projection angle is 39.3 degrees.
Explanation:
We can start using the definition of displacement in one dimension between any 2 points which is the difference between them, so we have
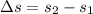
And apply it to get the horizontal and vertical displacements.
Once we have found them, we can use trigonometric functions to find the projection angle with respect the horizontal.
Linear displacements.
Using the definition of displacement, we can write the horizontal displacement as
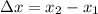
So we can use the given points
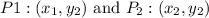 on the displacement formula
on the displacement formula
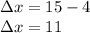
In the same manner we can look at the y components of those points to find the vertical displacement
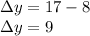
Thus the horizontal displacement is 11 units and the vertical displacement is 9 units.
Projection angle.
The projection angle with respect the horizontal is the angle that is made between the line that connects the points P1 and P2 and the horizontal, so we can use the linear displacements previously found to write
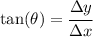
Solving for the angle we get
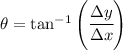
Replacing values
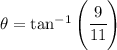
Which give us
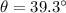
So the projection angle is 39.3 degrees.