Question

A discuss moves from P1 (4,8) to P2 (15,17). What is the lincar displacement in the horizontal and vertical directions? What is the angle of projection? 6)

Answer 1

The horizontal displacement is 11 units, the vertical displacement is 9 units, and the projection angle is 39.3 degrees.

Explanation:

We can start using the definition of displacement in one dimension between any 2 points which is the difference between them, so we have

`\Delta s = s_2-s_1`

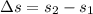
And apply it to get the horizontal and vertical displacements.

Once we have found them, we can use trigonometric functions to find the projection angle with respect the horizontal.

Linear displacements.

Using the definition of displacement, we can write the horizontal displacement as

`\Delta x = x_2-x_1`

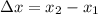
So we can use the given points
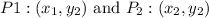`P1:(x_1,y_2)  \text{  and  } P_2: (x_2,y_2)` on the displacement formula

`\Delta x = 15-4\\\Delta x = 11`

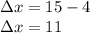
In the same manner we can look at the y components of those points to find the vertical displacement

`\Delta y = 17-8\\\Delta y =9`

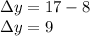
Thus the horizontal displacement is 11 units and the vertical displacement is 9 units.

Projection angle.

The projection angle with respect the horizontal is the angle that is made between the line that connects the points P1 and P2 and the horizontal, so we can use the linear displacements previously found to write

`\tan(\theta) = \cfrac{\Delta y}{\Delta x}`

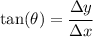
Solving for the angle we get

`\theta = \tan^(-1)\left(\cfrac{\Delta y}{\Delta x}\right)`

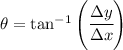
Replacing values

`\theta = \tan^(-1)\left(\cfrac{9}{11}\right)`

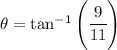
Which give us

`\theta = 39.3^\circ`

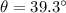
So the projection angle is 39.3 degrees.