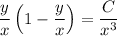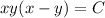Question

Find the general solution of the equation: (y^2-2xy)dx + (2xy-x^2)dy = 0

Answer 1

The ODE is exact, since

`(\partial(y^2-2xy))/(\partial y)=2y-2x`

`(\partial(2xy-x^2))/(\partial x)=2y-2x`

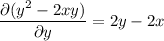
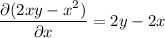
so there is solution
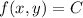`f(x,y)=C` such that

`(\partial f)/(\partial x)=y^2-2xy`

`(\partial f)/(\partial y)=2xy-x^2`

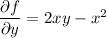
Integrating both sides of the first PDE wrt
`x` gives

`f(x,y)=xy^2-x^2y+g(y)`

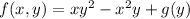
Differentiating both sides wrt
`y` gives

`(\partial f)/(\partial y)=2xy-x^2+(\mathrm dg)/(\mathrm dy)=2xy-x^2`

`\implies(\mathrm dg)/(\mathrm dy)=0\implies g(y)=C`

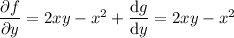
Then the solution to the ODE is

`f(x,y)=\boxed{xy^2-x^2y=C}`

# # #

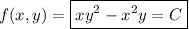
Alternatively, we can see that the ODE is homogeneous, since replacing
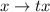`x\to tx` and
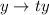`y\to ty` reduces to the same ODE:

`((ty)^2-2(tx)(ty))\,\mathrm d(tx)+(2(tx)(ty)-(tx)^2)\,\mathrm d(ty)=0`

`t^3(y^2-2xy)\,\mathrm dx+t^3(2xy-x^2)\,\mathrm dy=0`

`(y^2-2xy)\,\mathrm dx+(2xy-x^2)\,\mathrm dy=0`

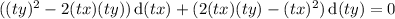
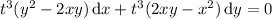
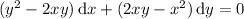
This tells us we can solve by substituting
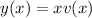`y(x)=xv(x)`, so that
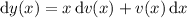`\mathrm dy(x)=x\,\mathrm dv(x)+v(x)\,\mathrm dx`, and the ODE becomes

`(x^2v^2-2x^2v)\,\mathrm dx+(2x^2v-x^2)(x\,\mathrm dv+v\,\mathrm dx)=0`

`v(v-2)\,\mathrm dx+(2v-1)(x\,\mathrm dv+v\,\mathrm dx)=0`

`3v(v-1)\,\mathrm dx+x(2v-1)\,\mathrm dv=0`

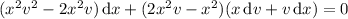
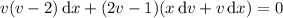
which is separable as

`(1-2v)/(3v(v-1))\,\mathrm dv=\frac{\mathrm dx}x`

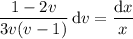
Integrating both sides gives

`-\frac13\ln|v(1-v)|=\ln|x|+C`

`v(1-v)=\frac C{x^3}`

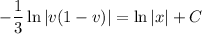
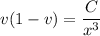
and solving in terms of
`y(x)`,

`\frac yx\left(1-\frac yx\right)=\frac C{x^3}`

`xy(x-y)=C`

`\boxed{x^2y-xy^2=C}`