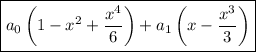I guess the ODE is supposed to be
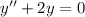
So if
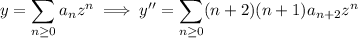
then
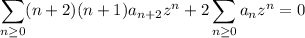
![\displaystyle\sum_(n\ge0)\bigg[(n+2)(n+1)a_(n+2)+2a_n\bigg]z^n=0](https://img.qammunity.org/2020/formulas/mathematics/college/r9s6g6gtbeudr72z5cht8x647jut8i1xwa.png)
so that
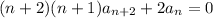
for
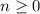 , or equivalently,
, or equivalently,
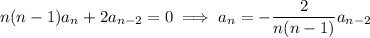
for
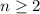 . Note the dependency between every other coefficient - this means we can consider two cases:
. Note the dependency between every other coefficient - this means we can consider two cases:
- If
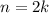 , where
, where
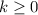 is an integer, then
is an integer, then
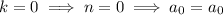
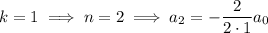
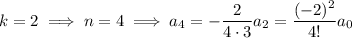
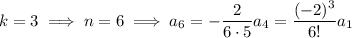
and so on, with
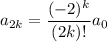
- If
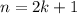 , then
, then
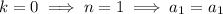
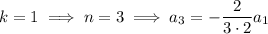
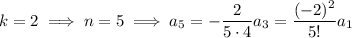
and so on, with
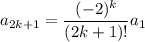
Then the ODE has solution
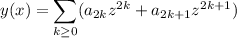
and the first six non-zero terms occur for
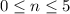 , for which we get
, for which we get