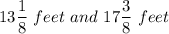Answer: The new dimensions of the garden are
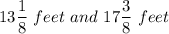
Explanation:
Since we have given that
Old length of rectangular garden =
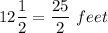
Old breadth of rectangular garden =
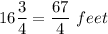
If
 feet is added to all the sides.
feet is added to all the sides.
So, New length of rectangular garden is given by
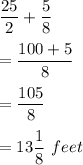
New breadth of rectangular garden is given by
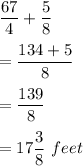
Hence, the new dimensions of the garden are