Question

A heat exchanger is to be constructed by forming copper tubing into a coil and placing the latter inside an insulated steel shell. In this exchanger, water will flow inside the tubing, and a hydrocarbon vapor at a rate of 0.126 kg/s will be condensing on the outside surface of the tubing. The inside and outside diameters of the tube are 0.0127 and 0.0152 m, respectively, Inlet and exit temperatures for the water are 10 and 32°C, respectively. The heat of conden- sation of the hydrocarbon at a condensing temperature of 88°C is 335 kJ/kg, and the heat- transfer coefficient for the condensing vapor is 1420 W/m².K. Heat losses from the shell may be neglected. What length of copper tubing will be required to accomplish the desired heat transfer?

Answer 1

Step-by-step explanation:

The given data is as follows.

Flow of mass rate of hydrocarbon, m = 0.126 kg/s

Heat of condensation, (
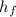`h_(f)`) = 335 kJ/kg

For water
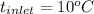`t_(inlet)= 10^(o)C`, and
`t_(out) = 32^(o)C`

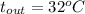
Formula for transfer of heat is as follows.

Q =
`m * h_(f)`

=
`0.126 kg/s * 335 kJ/kg`

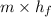
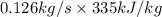
= 41.875 kJ/s

Also, it is known that Q =
`h * A * (\Delta T)_(lmtd)`

As it is given that for condensing T =
`88^(o)C`.

`(\Delta T)_(lmtd)` =
`(\Delta T_(1) - \Delta T_(2))/(ln (\Delta T_(1))/(\Delta T_(2)))`

=
`((78 - 56))/(ln (78)/(56))`

=
`((78 - 56))/(0.33)`

=
`66.67 ^(o)C`

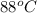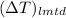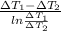
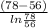
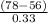
As it is given that inside and outside diameters of the tube are as follows.

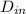`D_(in)` = 0.0127, and
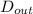`D_(out)` = 0.0152 m

Formula for A =
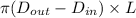`\pi (D_(out) - D_(in)) * L` ......... (1)

Hence, putting value of equation (1) in the following formula.

Q =
`h * A * (\Delta T)_(lmtd)`

41.875 kJ/s =
`1420 W/m^(2) * 3.14 * (0.0152 - 0.0127)m * L * 66.67 ^(o)C`

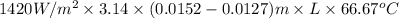
L = \frac{41.875 \times 1000 J/s}{743.17 W^{o}C}

= 56.34 h

Thus, we can conclude that length of copper tubing will be required to accomplish the desired heat transfer 56.34 h.