Question

If you could please help me? I have been having a really hard time so far. I would reallly appreciate if you could explain how to do the problems.

Thank you!

Answer 1

I will set up question 1 and do question 2, which is easier to solve.

Question 1

To determine if a function is one-to-one, we must prove that f(a) = f(b). In other words, if you get the same y value by plugging a into the function as you do by plugging b, then the function is one-to-one. I will partially do the first one and let you do the rest on your own.

f(x) = (x - 1)/(3x + 3)

f(a) = (a - 1)/(3(a) + 3)

f(a) = (a - 1)/(3a + 3)

f(a) = (a - 1)/[3(a + 1)]

Now do f(b).

f(b) = (b - 1)/[3(b + 1)]

Set f(a) = f(b). If after doing the math you end up with a = b, then you will know that this function is one-to-one.

Take it from here and do the same for all functions listed.

Question 2

Let cbrt = cube root for short.

cbrt{x - 2} + 8

Let y = f(x)

y = cbrt{x- 2} + 8

Switch x and y.

x = cbrt{y - 2} + 8

x - 8 = cbrt{y - 2}

Cube both sides.

(x - 8)^3 = [cbrt{y - 2}]^3

(x - 8)^3 = y - 2

Solve for y.

(x - 8)^3 + 2 = y

Replace y with f^(-1) x.

f^(-1) x = (x - 8)^3 + 2

Answer: Choice 1

Answer 2

2.

Explanation:

1. Recall the definition of one-to-one function. We say that
`f` is one-to-one if and only if the equality
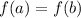`f(a)=f(b)` implies that
`a=b`.

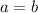First example:
`f(x)=(x-1)/(3x+3)`.

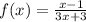We start with

`f(a) = (a-1)/(3a+3) = (b-1)/(3b+3) = f(b)`.

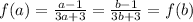In the above equalities, the central one, making cross products, is equivalent to

`(a-1)(3b+3) = (3a+3)(b-1)`.

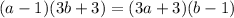Then,
`3ab+3a-3b-3 = 3ab-3a+3b-3`. Now, cancelling identical terms we get
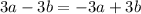`3a-3b=-3a+3b` which is equivalent to
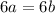`6a=6b`. Thus, simplifying the factor 6, we get
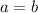`a=b`. Therefore, the function is one-to-one.

Second example:
`f(x) = √(5x+9)`.

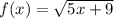We try to follow the same reasoning. We start with

`√(5a+9) = √(5b+9)`.

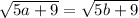Now, we elevate both members to the square (recall that both expressions are positive, so there is no problem with squaring) and obtain:

`5a+9=5b+9`. We eliminate the 9's and we get
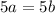`5a=5b`. Simplifying the 5's, we finally obtain that
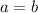`a=b`. Therefore the function is one-to-one.

Third example.
`f(x) = (7)/(4x^2)`.

This example is different from the previous ones. Recall that we prove that a function is not one-to-one if we find two different numbers
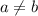`a\\eq b` such that
`f(a)=f(b)`.

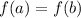Then, notice that if we take
`a=-1` and
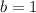`b=1` we get that

`f(-1) = (7)/(4(-1)^2) = (7)/(4)` and
`f(-1) = (7)/(4\cdot 1^2) = (7)/(4)`.

Then, this function is not one-to-one.

Fourth example:
`f(x) = (1)/(2)x^3`.

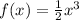As the first two cases. Consider
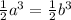`(1)/(2)a^3=(1)/(2)b^3`. Then, simplify the factor 1/2, and we get
`a^3=b^3`.

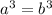Now, let us transform the previous equality into
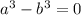`a^3-b^3=0`. This expression can be factored:
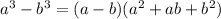`a^3-b^3=(a-b)(a^2+ab+b^2)`. Thus,

`0=(a-b)(a^2+ab+b^2)`

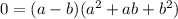
Notice that the above equality is possible if and only if
`a-b=0` or

`a^2+ab+b^2=0`. But the second possibility is impossible (you can check it using the general formula for second degree equations), thus, necessarily
`a-b=0` which is equivalent to
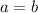`a=b`. Therefore, the function is one-to-one.

Fifth example:
`f(x) = 3x^4+7x^3`.

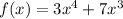First, notice that the polynomial
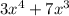`3x^4+7x^3` can be factored as

`3x^4+7x^3 = x^3(3x+7)`.

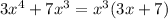From here is not difficult to deduce that
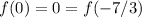`f(0)=0=f(-7/3)` and consequently the function is not one-to-one.

2. As we are looking for the inverse function
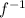`f^(-1)` of
`f(x)` is a better idea to use the following notation:

`y = \sqrt[3]{x-2} + 8`,

instead of
`f(x)`.

Notice that, with this notation we are saying that
`y` depends on
`x`. Now, when we are looking for the inverse function we will try to write the variable
`x` in terms of
`y`. With this idea, the first step is to move the 8 in the right hand side to the left hand side, so:

`y-8 = \sqrt[3]{x-2}`.

Recall that we need to isolated the variable
`x`, so we must ‘‘eliminate’’ the cubic root. In order to do this we take cubic powers in both side of the above equality. Then,

`(y-8)^3 = x-2`.

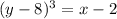Finally, we take the 2 to the left hand side and we get

`x = (y-8)^3+2`.

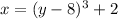Thus, the inverse function is
`f^(-1)(x) = (x-8)^3+2`.

Notice that if we do
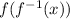`f(f^(-1)(x))` we get
`x`.