Answer:
2.
Explanation:
1. Recall the definition of one-to-one function. We say that
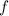 is one-to-one if and only if the equality
is one-to-one if and only if the equality
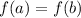 implies that
implies that
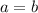 .
.
First example:
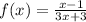 .
.
We start with
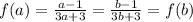 .
.
In the above equalities, the central one, making cross products, is equivalent to
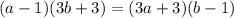 .
.
Then,
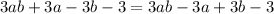 . Now, cancelling identical terms we get
. Now, cancelling identical terms we get
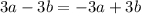 which is equivalent to
which is equivalent to
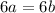 . Thus, simplifying the factor 6, we get
. Thus, simplifying the factor 6, we get
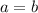 . Therefore, the function is one-to-one.
. Therefore, the function is one-to-one.
Second example:
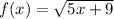 .
.
We try to follow the same reasoning. We start with
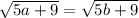 .
.
Now, we elevate both members to the square (recall that both expressions are positive, so there is no problem with squaring) and obtain:
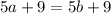 . We eliminate the 9's and we get
. We eliminate the 9's and we get
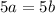 . Simplifying the 5's, we finally obtain that
. Simplifying the 5's, we finally obtain that
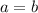 . Therefore the function is one-to-one.
. Therefore the function is one-to-one.
Third example.
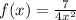 .
.
This example is different from the previous ones. Recall that we prove that a function is not one-to-one if we find two different numbers
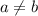 such that
such that
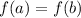 .
.
Then, notice that if we take
 and
and
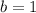 we get that
we get that
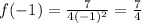 and
and
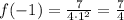 .
.
Then, this function is not one-to-one.
Fourth example:
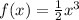 .
.
As the first two cases. Consider
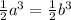 . Then, simplify the factor 1/2, and we get
. Then, simplify the factor 1/2, and we get
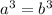 .
.
Now, let us transform the previous equality into
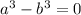 . This expression can be factored:
. This expression can be factored:
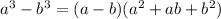 . Thus,
. Thus,
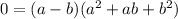
Notice that the above equality is possible if and only if
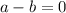 or
or
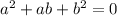 . But the second possibility is impossible (you can check it using the general formula for second degree equations), thus, necessarily
. But the second possibility is impossible (you can check it using the general formula for second degree equations), thus, necessarily
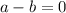 which is equivalent to
which is equivalent to
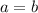 . Therefore, the function is one-to-one.
. Therefore, the function is one-to-one.
Fifth example:
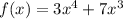 .
.
First, notice that the polynomial
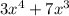 can be factored as
can be factored as
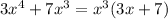 .
.
From here is not difficult to deduce that
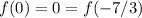 and consequently the function is not one-to-one.
and consequently the function is not one-to-one.
2. As we are looking for the inverse function
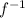 of
of
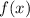 is a better idea to use the following notation:
is a better idea to use the following notation:
![y = \sqrt[3]{x-2} + 8](https://img.qammunity.org/2020/formulas/mathematics/high-school/8baa4lpwms01lh5q44496reuq12wrvfofk.png) ,
,
instead of
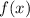 .
.
Notice that, with this notation we are saying that
 depends on
depends on
 . Now, when we are looking for the inverse function we will try to write the variable
. Now, when we are looking for the inverse function we will try to write the variable
 in terms of
in terms of
 . With this idea, the first step is to move the 8 in the right hand side to the left hand side, so:
. With this idea, the first step is to move the 8 in the right hand side to the left hand side, so:
![y-8 = \sqrt[3]{x-2}](https://img.qammunity.org/2020/formulas/mathematics/high-school/ci6nstqooilwkh4pbwdboye2ybeeoehyke.png) .
.
Recall that we need to isolated the variable
 , so we must ‘‘eliminate’’ the cubic root. In order to do this we take cubic powers in both side of the above equality. Then,
, so we must ‘‘eliminate’’ the cubic root. In order to do this we take cubic powers in both side of the above equality. Then,
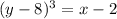 .
.
Finally, we take the 2 to the left hand side and we get
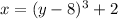 .
.
Thus, the inverse function is
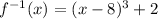 .
.
Notice that if we do
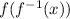 we get
we get
 .
.