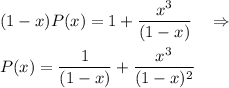Answer:
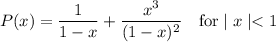 [/tex]
[/tex]
Explanation:
The generating function of a sequence is the power series whose coefficients are the elements of the sequence. For the sequence
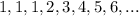
the generating function would be
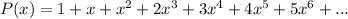
we can multiply P(x) by x to get
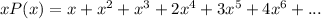
Note that
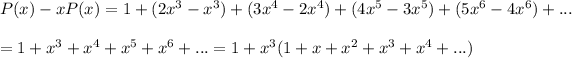
which for
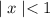 can be rewritten as
can be rewritten as