Answer:
velocity = 50m/s
distance = -83.33m
Step-by-step explanation:
The velocity of the particle is given by;
v = 20t² - 100t + 50 -------------------(i)
Since acceleration is the time rate of change in velocity, to get the acceleration (a), we find the derivative of equation (i) with respect to t as follows;
a =
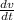 =
=
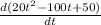
a = 40t - 100 ------------------(ii)
Now, when a = 0, let's find the time t by substituting the value of a into equation (ii) as follows;
0 = 40t - 100
=> 40t = 100
=> t =
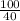
=> t = 2.5seconds.
This means that at t = 2.5 seconds, the acceleration of the particle is zero(0)
(a) Now, to get the velocity at this instant (t = 2.5s), substitute the value of t into equation (i) as follows;
v = 20(0)² - 100(0) + 50
v = 0 - 0 + 50
v = 50 m/s
Therefore, the velocity when a is zero is 50m/s
(b) To get the distance (s) travelled at that instant, we integrate equation (i) as follows;
s =
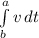 -----------------------(iii)
-----------------------(iii)
Where;
a = the time instant = 2.5 seconds
b = the initial time instant = 0
v = 20t² - 100t + 50
Substitute these values into equation (iii) as follows;
s =
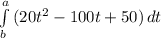
s =
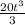 -
-
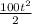 + 50t
+ 50t
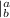
Substitute the values of a and b as follows;
s = [
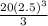 -
-
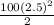 + 50(2.5)] - [
+ 50(2.5)] - [
 -
-
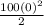 + 50(0)]
+ 50(0)]
s = [
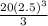 -
-
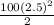 + 50(2.5)] - 0
+ 50(2.5)] - 0
s = 104.17 - 312.5 + 125
s = -83.33m
Therefore, the distance traveled at that instant is -83.33m