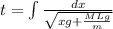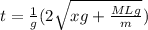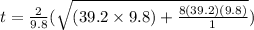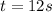Question

A rope of total mass m hnd length L is suspended vertically with an object of mass M suspended from the lower end. Find an expression tor the wave speed at any point a distance x from the lower end. and calculate the time needed for the transverse pulse to travel the length of the rope. The rope has a length of 39.2 m and a mass of 1.00 kg. Suspended object has a mass of 8.00 kg.

Answer 1

Part a)

`v = \sqrt{xg + (MLg)/(m)}`

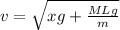
Part b)

t = 12 s

Step-by-step explanation:

Part a)

Tension in the rope at a distance x from the lower end is given as

`T = (m)/(L)xg + Mg`

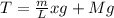
so the speed of the wave at that position is given as

`v = \sqrt{(T)/(\mu)}`

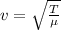
here we know that

`\mu = (m)/(L)`

now we have

`v = \sqrt{( (m)/(L)xg + Mg)/(m/L)`

`v = \sqrt{xg + (MLg)/(m)}`

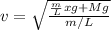
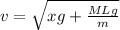
Part b)

time taken by the wave to reach the top is given as

`t = \int \frac{dx}{\sqrt{xg + (MLg)/(m)}}`

`t = (1)/(g)(2\sqrt{xg + (MLg)/(m)})`

`t = (2)/(9.8)(\sqrt{(39.2* 9.8) + (8(39.2)(9.8))/(1)})`

`t = 12 s`