Answer:
Bore = 7 cm
stroke = 6.36 cm
compression ratio = 10.007
Step-by-step explanation:
Given data:
Cubic capacity of the engine, V = 245 cc
Clearance volume, v = 27.2 cc
over square-ratio = 1.1
thus,
D/L = 1.1
where,
D is the bore
L is the stroke
Now,
V =

or
V =
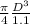
on substituting the values, we have
245 =
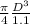
or
D = 7.00 cm
Now,
we have
D/L = 1.1
thus,
L = D/1.1
L = 7/1.1
or
L= 6.36 cm
Now,
the compression ratio is given as:
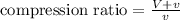
on substituting the values, we get
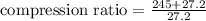
or
Compression ratio = 10.007