Answer:
The numbers are
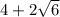 and
and
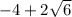
Explanation:
Let
x ------> one number
(x-8) ------> the another number
we know that
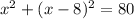
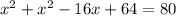
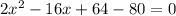

Simplify
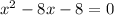
The formula to solve a quadratic equation of the form
 is equal to
is equal to

in this problem we have
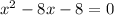
so
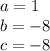
substitute in the formula
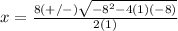
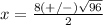
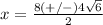

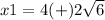
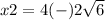
so
the solution must be a positive real number
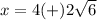
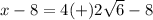 ------>
------>
