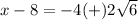Question

a positive real number is 8 less than another. if the sum of the squares of the two numbers is 80 find the numbers

Answer 1

The numbers are

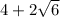`4+2√(6)` and
`-4+2√(6)`

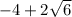
Explanation:

Let

x ------> one number

(x-8) ------> the another number

we know that

`x^(2) +(x-8)^(2)=80`

`x^(2) +x^(2)-16x+64=80`

`2x^(2)-16x+64-80=0`

`2x^(2)-16x-16=0`

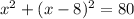
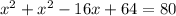
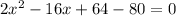
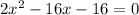
Simplify

`x^(2)-8x-8=0`

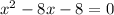
The formula to solve a quadratic equation of the form
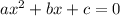`ax^(2) +bx+c=0` is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}} {2a}`

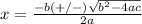
in this problem we have

`x^(2)-8x-8=0`

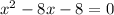
so

`a=1\\b=-8\\c=-8`

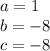
substitute in the formula

`x=\frac{8(+/-)\sqrt{-8^(2)-4(1)(-8)}} {2(1)}`

`x=\frac{8(+/-)√(96)} {2}`

`x=\frac{8(+/-)4√(6)} {2}`

`x=4(+/-)2√(6)`

`x1=4(+)2√(6)`

`x2=4(-)2√(6)`

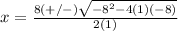
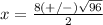
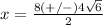
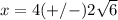
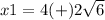
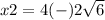
so

the solution must be a positive real number

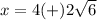
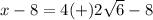`x=4(+)2√(6)`

`x-8=4(+)2√(6)-8` ------>
`x-8=-4(+)2√(6)`