Answer:
The football must be launched whit an angle of 20,487 degrees to reach a maximum height of 10 meters.
Step-by-step explanation:
To solve this problem we use the parabolic motion equations:
We define:
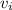 : total initial speed =
: total initial speed =
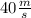
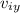 :initial speed component in vertical direction (y) =
:initial speed component in vertical direction (y) =
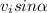
 : vertical speed at any point on the parabolic path
: vertical speed at any point on the parabolic path
g= acceleration of gravity= 9,8
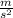
 = angle that forms the total initial velocity with the ground
= angle that forms the total initial velocity with the ground
Equation of the speed of the football in the vertical direction :
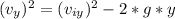 Equation (1)
Equation (1)
We replace
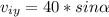 ,
,
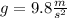 in the equation (1):
in the equation (1):
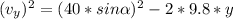 Equation(2)
Equation(2)
Angle calculation
The speed of the football in the vertical direction gradually decreases until its value is zero when it reaches the maximum height.
We replace
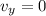 ,
,
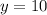 in the equation (2)
in the equation (2)
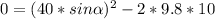
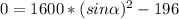

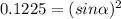
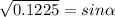
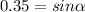
 °
°
Answer:The football must be launched whit an angle of 20,487 degrees to reach a maximum height of 10 meters.