Question

A football is launched at 40 m/s, at an angle from the ground. What should the angle be such that maximum height of the trajectory of the football is 10 m?

Answer 1

The football must be launched whit an angle of 20,487 degrees to reach a maximum height of 10 meters.

Step-by-step explanation:

To solve this problem we use the parabolic motion equations:

We define:

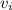`v_(i)`: total initial speed =
`40(m)/(s)`

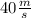
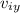`v_(iy)`:initial speed component in vertical direction (y) =
`v_(i) sin\alpha`

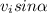
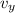`v_(y)`: vertical speed at any point on the parabolic path

g= acceleration of gravity= 9,8
`(m)/(s^(2) )`

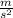
`\alpha`= angle that forms the total initial velocity with the ground

Equation of the speed of the football in the vertical direction :

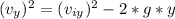`(v_(y) )^(2)=(v_(iy) )^(2) -2*g*y` Equation (1)

We replace
`v_(iy) =40*sin\alpha`,
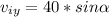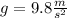`g=9.8(m)/(s^(2) )` in the equation (1):

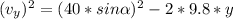`(v_(y) )^(2) =(40*sin\alpha )^(2) -2*9.8*y` Equation(2)

Angle calculation

The speed of the football in the vertical direction gradually decreases until its value is zero when it reaches the maximum height.

We replace
`v_(y) =0` ,
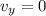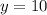`y=10` in the equation (2)

`0=(40*sin\alpha )^(2) -2*9.8*10`

`0=1600*(sin\alpha )^(2) -196`

`(196)/(1600) =(sen\alpha )^(2)`

`0.1225=(sin\alpha )^(2)`

`√(0.1225) =sin\alpha`

`0.35=sin\alpha`

`\alpha =20.487` °

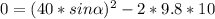
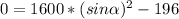
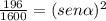
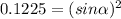
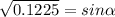
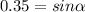
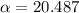Answer:The football must be launched whit an angle of 20,487 degrees to reach a maximum height of 10 meters.