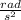Answer:
angular acceleration=
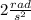
Step-by-step explanation:
Kinematic equation for uniformly accelerated circular motion:
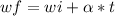
wf=final angular speed
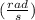
wi=initial angular speed
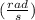
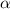 = angular acceleration
= angular acceleration
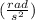
We replace wf=10
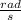 ,wi=0, t=5s in the equation(1):
,wi=0, t=5s in the equation(1):
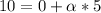
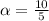
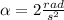
The angular acceleration is 2