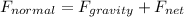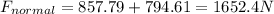Question

A circular-motion addict of mass 81.0 kg rides a Ferris wheel around in a vertical circle of radius 10.0 m at a constant speed of 6.10 m/s. (a) What is the period of the motion? What is the magnitude of the normal force on the addict from the seat when both go through (b) the highest point of the circular path and (c) the lowest point?

Answer 1

(a) 10.29 sec (b) 63.19 N (c)1652.4 N

Step-by-step explanation:

We have given mass m =81 kg

Radius r = 10 m

Velocity v = 6.10 m/sec

(a) Time period of the motion
`T=(2\pi r)/(v)=(2* 3.14* 10)/(6.10)=10.29sec`

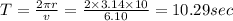
(b) At highest point net force
`F_(net)=F_(normal)-F_(gravity)`
`F_net=F_(gravity)+F_(normal)`

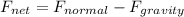
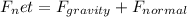
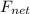`F_(net)` is given by
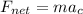`F_(net)=ma_c` where
`a_c` is centripetal acceleration

`a_c=(v^2)/(r)=(10.29^2)/(10)=10.59 m/sec^2`

So
`F_(net)=81* 10.59=857.79\ N`

`F_(gravity)=81* 9.81=794.61\ N`

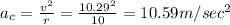
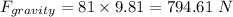
So
`F_(normal)=857.79-794.61=63.19[/text]</p><p>(c) At lowest point [tex]F_(net)=F_(normal)-F_(gravity)`

So
`F_(normal)=F_(gravity)+F_(net)`

`F_(normal)=857.79+794.61=1652.4 N`