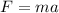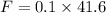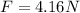Answer:
Step-by-step explanation:
Let the coefficient of restitution is "e"
so we have
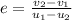
here we have

now we have by momentum conservation
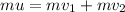
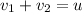
now we have
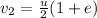

now we have the ratio of final kinetic energy and initial kinetic energy given as 0.86
so we have
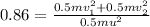


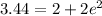
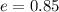
so we have
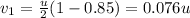
now change in velocity of first ball is given as

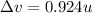
now acceleration of the ball is given as
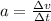

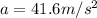
so the force on the ball during collision is