Question

1. Evaluate the function f(x)=3x-1 using the domain of -2, 0, 3, and 5. Results are to be shown in a table.

2. Determine the domain of the inverse of the function given in problem 2. Explain the reasoning.

Answer 1

Explanation:

1) . The given function is f(x) = 3x - 1

Using the domain or value of x = -2, 0, 3, and 5 we have to formulate a table for the value of the function.

f(-2) = 3(-2) - 1

= -7

f(0) = 3×0 - 1

= -1

f(3) = 3(3) - 1

= 9 - 1

= 8

f(5) = 3(5) - 1

= 15 - 1

= 14

x -2 0 3 5

y -7 -1 8 14

2). Since f(x) = 3x - 1

Now we can rewrite the function in the form of an equation.

y = 3x - 1

To formulate the inverse of the given function we will flip x by y.

x = 3y - 1

then we will solve it for the value of y.

3y = x + 1

y =
`(1)/(3)(x + 1)`

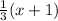
Or
`f^(-1)(x)=(1)/(3)(x+1)`

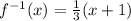
Now this inverse function will be defined for all real numbers.

Therefore, domain of
`f^(-1)(x)` will be all real numbers.

Answer 2

See explanation

Explanation:

You are given the function
`f(x)=3x-1`

The domain of the function are all possible values of variable x, so you can find f(x) for x=-2, 0, 3, 5:

`f(-2)=3\cdot (-2)-1=-6-1=-7\\ \\f(0)=3\cdot 0-1=0-1=-1\\ \\f(3)=3\cdot 3-1=9-1=8\\ \\f(5)=3\cdot 5-1=15-1=14`

The table is

`\begin{array}{cc}x&f(x)\\-2&-7\\0&-1\\3&8\\5&14\end{array}`

The inverse function
`f^(-1)(x)` has the domain which is the range of the function f(x) (all possible values of f(x)), so the domain of inverse function is {-7,-1,8,14}