The statement that
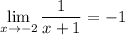
is equivalent to saying that, for any
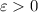 , there exists
, there exists
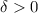 such that if
such that if
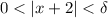
then it's guaranteed that

We want to pick
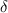 to make this guarantee.
to make this guarantee.
We have
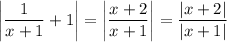
If we assume
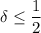 , then
, then
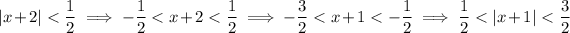
The lower bound on
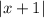 is what's important here, because its gives us an upper bound on the reciprocal:
is what's important here, because its gives us an upper bound on the reciprocal:
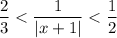
Then in the expected
 -inequality, we have
-inequality, we have
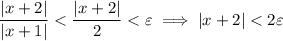
Comparing this to our chosen
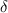 -inequality, this suggests we should pick
-inequality, this suggests we should pick
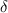 to be the smaller of
to be the smaller of
 and
and
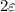 , or
, or
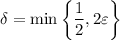 .
.
# # #
Now for the proof itself. Let
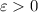 be given, and assume
be given, and assume
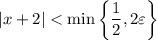 .
.
- If
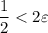 , then
, then
 and
and
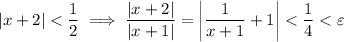
- If
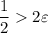 , then
, then
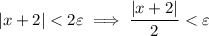
and
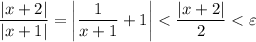
This completes the proof.