Question

The illuminance of a surface varies inversely with the square of its distance from the light source.If the illuminance of a surface is 120 lumens per square meter when its distance from a certain light source is 6 meters, by how many meters should the distance of the surface from the source be increased to reduce its illuminance to 30 lumens per square meter?

Answer 1

Distance between the surface and source of light will be increased by 6 meters.

Explanation:

The illuminance of a surface varies inversely with the square of ts distance from the light source.

Let illuminance of the surface = x lumens per square meter

and distance from a light source = y meter.

Now x ∝
`(1)/(y^(2) )`

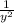
Or
`x=(k)/(y^(2) )` [k = proportionality constant]

Now we will find the value of k.

k = xy²

k = 120×(6)²

k = 4320

We have to calculate the distance of the source if illuminance of the surface is 30 lumens per square meter.

`30=(4320)/(y^(2))`

y² =
`(4320)/(30)`

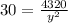
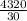
y² = 144

y = √144 = 12 meters

So the source of the light will be shifted away from the surface = 12 - 6 = 6 meters.