Question

What is the smallest integer that can be divided by the product of a prime number and 7 while yielding a prime number?

(A) 7
(B) 14
(C) 24
(D) 28
(E) 35

Answer 1

(D). 28

Explanation:

We have been given that the smallest integer that can be divided by the product of a prime number and 7 while yielding a prime number.

We know that smallest prime is 2. The product of 2 and 7 is 14.

Let us divide our given numbers by 14.

(A) 7.

`(7)/(14)=(1)/(2)`

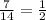
The quotient is not a integer or prime number.

(B). 14

`(14)/(14)=1`

We know that 1 is not a prime number.

(C) 24.

`(24)/(14)=(12)/(7)`

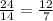
The quotient is not a integer or prime number.

(D). 28

`(28)/(14)=2`

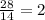
Since 2 is a prime number, therefore, 28 is the smallest integer that can be divided by the product of a prime number and 7 and yield a prime number.