Question

the area of the rectangle is 96 square feet if the length is 2 times the width, then find the dimensions of the rectangle round off your answers to the nearest hundredths

Answer 1

Explanation:

1. The area of rectangle is equal to A*B, where A is the length of rectangle, and B the width( or vice versa).

2. If A = 2B, then area = 2A*A =2A^2=96. Simplify A^2=48.

3. Taking square root of 48 we get A = 6.928203 -> Rounding off to the nearest hundredths we have A = 6.93, and B = 3.465 =3.47(Rounded off).

Answer 2

The length of rectangle is approximately 13.86 feet and width is 6.93 feet.

Explanation:

Let x represent width of the rectangle.

We have been given that the length is 2 times the width, then length would be
`2x`.

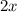We have been given that the area of the rectangle is 96 square feet.

We know that area of rectangle is length times width, so we can represent this information in an equation as:

`2x\cdot x=96`

`2x^2=96`

`(2x^2)/(2)=(96)/(2)`

`x^2=48`

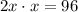
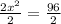
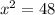
Take square root of both sides:

`x=\pm √(48)`

`x=\pm 6.92820`

`x\approx \pm 6.93`

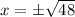
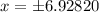
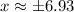
Since width cannot be negative, therefore, the width of the rectangle would be 6.93 feet.

The length is 2 times width, so length would be:

`2* 6.93\approx 13.86`

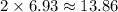
Therefore, the length of rectangle is approximately 13.86 feet.