Answer:
y =

Explanation:
Let the total numbers are n.
If the average of y numbers is x then we can form an equation
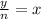
⇒
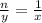
⇒ n =
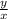 --------(1)
--------(1)
Now 30 is added to the set of numbers then average becomes (x - 5)
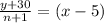
⇒
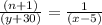
⇒ (n + 1) =
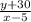
⇒ n =
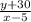 - 1 ----- (2)
- 1 ----- (2)
Now we equate the values of n from equation 1 and 2
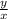 =
=
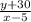 - 1
- 1
y(x - 5) = x(y + 30) - x(x - 5) [ By cross multiplication ]
xy - 5y = xy + 30x - x² + 5x
xy - xy - 5y = 35x - x²
-5y = 35x - x²
x² - 35x = 5y
y =
