Answer:
The box of length
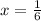 must be cut from each corner to maximize the volume.
must be cut from each corner to maximize the volume.
Explanation:
It is given that the side of a square card board is 1 m.
Let small squares of length x are cut from the four corners. The dimensions of the box are
Length = (1-2x) m
Width = (1-2x) m
Height = x m
The volume of a cuboid is

where, l is length and b is breadth and h is height.
The volume of a rectangular box.
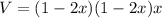
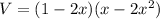
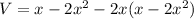
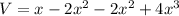

We need to maximize the volume. Differential above equation with respect to x.
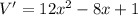 .... (1)
.... (1)
Equate V'=0 to find the critical points.
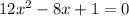

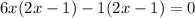
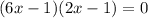
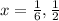
Differential equation (1) with respect to x.
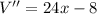
At
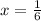
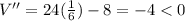
Volume is maximum at
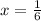 .
.
At
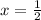

Volume is minimum at
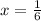 .
.
Therefore the box of length
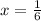 must be cut from each corner to maximize the volume.
must be cut from each corner to maximize the volume.