Step-by-step explanation:
It is given that,
Time taken by a planet to orbit a star,
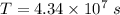
Radius of circular orbit,
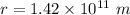
(a) Angular speed,
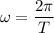
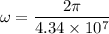
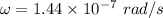
(b) Tangential speed of the planet,
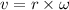

v = 20448 m/s
(c) Centripetal acceleration of the planet,
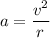
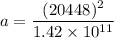
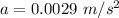
Hence, this is the required solution.