Answer:
0.567 (rounded to 3 decimal places)
Explanation:
Number of men enrolled in Calculus = 85
Number of women enrolled in Calculus = 65
Total students enrolled in Calculus = 85 + 65 = 150
We have to find the probability that if a calculus student is chosen at random, he is a man.
Total possible outcomes would be the total number of students in Calculus which is 150.
Favorable outcome would be the number of men in the class which would be 85.
The formula for probability is:
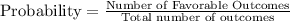
Using the values, we get:
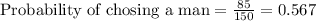
Thus, If a single calculus student is chosen the probability that he is a man is 0.567 (rounded to 3 decimal places)