Question

Is integer x<−20 ? x2+40x+391=0 x2=529 Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient EACH statement ALONE is sufficient to answer the question asked Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed

Answer 1

Both statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient.

Explanation:

Solving the equation of statement (1) with the quadratic formula:

`x_(1,2)=(-b\pm√(b^2-4ac))/(2a)`

`x^2+40x+391=0\\x_(1,2)=(-40\pm√(40^2-4(1)(391)))/(2(1))\\x_(1,2)=(-40\pm√(1600-1564))/(2)\\x_(1,2)=(-40\pm√(36))/(2)\\x_(1)=(-40+6)/(2)=(-34)/(2)=-17\\x_(1)=(-40-6)/(2)=(-46)/(2)=-23\\`

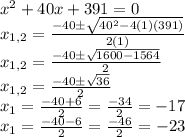
In this equation, one of the values of x is bigger than -20 but the other is smaller, this statement doesn't give enough information to answer the question.

Solving the quadratic equation of the statement (2):

`x^2=529\\x_(1,2)=\pm√(529) \\x_1=√(529)=23\\x_2=-√(529)=-23`

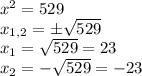
Again, one of the values of x is bigger than -20 and the other is smaller than -20. But if the information of this statement is considered along with the other x must be equal to -23, that is the value that appears as an answer in both equations, and with this information is possible to answer the question.