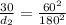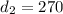Answer:
270 m
Step-by-step explanation:
When the driver hits the brakes, the kinetic energy of the car is converted by friction into heat. The kinetic energy K is given by:
(1)
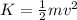
The work W done by friction is:
(2)

where the force of friction is:
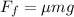
d: distance sliding
μ: friction coefficient
m: mass
g: gravitational constant
setting equation 1 and 2 equal:
(3)
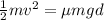
simplifying:
(4)
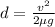
Use equation 4 to find the ratio between the two cases gives:
(5)
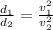
plugging in: