Question

1. Main Show Tank Calculation:

The main show tank has a radius of 70 feet and forms a quarter sphere where the bottom of the pool is spherical and the top of the pool is flat. (Imagine cutting a sphere in half vertically and then cutting it in half horizontally.) What is the volume of the quarter-sphere shaped tank? Round your answer to the nearest whole number. You must explain your answer using words, and you must show all work and calculations to receive credit.
Holding Tank Calculations:

2. The holding tanks are congruent. Each is in the shape of a cylinder that has been cut in half vertically. The bottom of each tank is a curved surface and the top of the pool is a flat surface. What is the volume of both tanks if the radius of tank #1 is 35 feet and the height of tank #2 is 120 feet? You must explain your answer using words, and you must show all work and calculations to receive credit.

3. The company is building a scale model of the theater’s main show tank for an investor's presentation. Each dimension will be made one sixth of the original dimension to accommodate the mock-up in the presentation room. What is the volume of the smaller mock-up tank?
4. Using the information from #4, answer the following question by filling in the blank: The volume of the original main show tank is ____% of the mock-up of the tank.

Answer 1

Explanation:

Volume of a sphere is

`(4)/(3) \pi {r}^(3)`

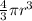
plug in 70 ft for the radius to get 1,436,755 cubic ft then divide that by 4 since the prompt describes a quarter sphere, giving you a tank volume of 359,189 cubic ft.

Volume of a cylinder is

`\pi {r}^(2) h`

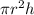
from the second prompt we know the tanks are identical since they are said to be congruent which means the hight and radius are the same. Plug in 120 f for h and 35 ft for r to get the volume of a cylinder and then divide that by 2 to get the volume of a single tank. the volume of both tanks would be

`\pi {35}^(2) (120) = 461,814`

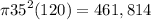
To show tank model is a sixth of the original so you divide the radius by 6 and perform the same calculation as in the first portion of the problem ro get the volume a quarter sphere

`(4)/(3) \pi {( (70)/(6) )}^(3) = 6,652 \: {ft}^(3)`

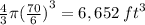
To get the percentage of the model relative to the original you divide the models volume by the full scale volume

`(6652)/(1436755) * 100 = 0.46`

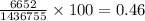
which is less than 1% of the full scale volume.