Answer:
Part 1)
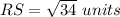
Part 2)
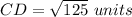
Part 3) The coordinates of endpoint C are (13,5)
Explanation:
Part 1) The endpoints of line RS are R(1, -3) and S(4,2). Find RS
we now that
the formula to calculate the distance between two points is equal to

substitute the values
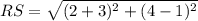

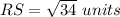
Part 2) The endpoints of line CD are C(-8,-1) and D(2,4). Find CD
we now that
the formula to calculate the distance between two points is equal to

substitute the values
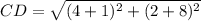

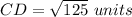
Part 3) The midpoint of line AC is M(5,6). One endpoint is A(-3,7). Find the coordinates of endpoint C
The formula to calculate the midpoint between two points is equal to
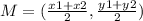
Let
(x2,y2)-------> the coordinates of point C
(x1,y1) -------> the coordinates of point A
substitute the given values
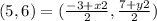
write the equations
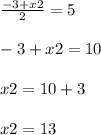
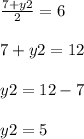
therefore
The coordinates of endpoint C are (13,5)