Question

What is the equation of the circle with center (3, 5) that passes through the point (–4, 10)?

Answer 1

Option 1:

`(x-3)^2+(y-5)^2 = 74`

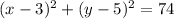
Explanation:

Given

Centre: (h,k) = (3,5)

Point on circle = (-4,10)

The distance between Centre and point on circle will be the radius of the circle

The distance formula will be used to calculate distance

`r = \sqrt{(x_2-x_1)^(2)+(y_2-y_1)^(2)}\\r = \sqrt{(-4-3)^(2)+(10-5)^(2)}\\r=\sqrt{(-7)^(2)+(5)^(2)}\\r=√(49+25)\\r=√(74)`

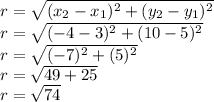
The standard equation of circle is:

`(x-h)^2+(y-k)^2=r^2`

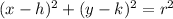
Putting the values of h,k and r

`(x-3)^2+(y-5)^2 = (√(74))^2\\(x-3)^2+(y-5)^2 = 74`

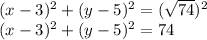
Hence, first option is correct ..