Answer:
Option 1:
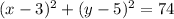
Explanation:
Given
Centre: (h,k) = (3,5)
Point on circle = (-4,10)
The distance between Centre and point on circle will be the radius of the circle
The distance formula will be used to calculate distance
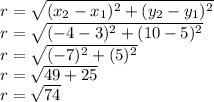
The standard equation of circle is:

Putting the values of h,k and r
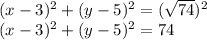
Hence, first option is correct ..