Answer:
Option 4: x^2+y^2 = 52
Explanation:
Given
Centre at origin
Point on circle = (-4, -6)
The distance between origin and point on circle will be the radius of the circle
So,
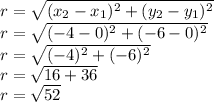
As the center is at origin the standard equation will be:
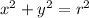
Putting the value of r
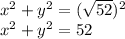
Hence, last option i.e. Option 4 is correct ..