Question

AB passes through A(-3, 0) and B(-6, 5). What is the equation of the line that passes through the origin and is parallel to ?

A.
5x − 3y = 0
B.
-x + 3y = 0
C.
-5x − 3y = 0
D.
3x + 5y = 0
E.
-3x + 5y = 0

Answer 1

For this case we have to by definition, if two lines are parallel then their slopes are equal.

We find the slope of the line AB:

`(x1, y1): (- 3,0)\\(x2, y2): (- 6,5)`

`m = \frac {y2-y1} {x2-x1} = \frac {5-0} {- 6 - (- 3)} = \frac {5} {- 6 + 3} = \frac {5} { -3} = - \frac {5} {3}`

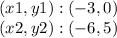
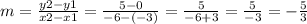
Thus, the parallel line is of the form:

`y = - \frac {5} {3} x + b`

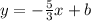
If the line passes through the origin, then we have the point (0,0):

`0 = - \frac {5} {3} (0) + b\\b = 0`

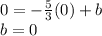
Then, the equation is:

`y = - \frac {5} {3} x\\3y = -5x\\3y + 5x = 0`

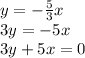
Answer:

OPTION C