bearing in mind that, parallel lines have the same slope, hmmm what's the slope of 9x - 3y = 27 anyway?
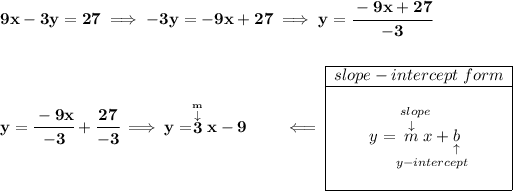
well, a parallel line to that one will also have the same slope, namely, we're really looking for the equation of al line whose slope is 3 and runs through (6,2).
