Answer:
C.
Explanation:
We are given
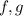 are odd which means:
are odd which means:
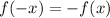
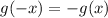
We can tell if a function,
 , is even if
, is even if
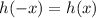 .
.
We can tell if a function,
 , is odd if
, is odd if
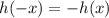 .
.
So let's test your I,II,III.
We will be replacing x with -x to find out.
I.
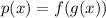
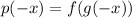
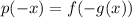
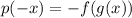
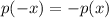
So
 is odd.
is odd.
II

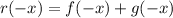
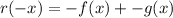
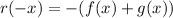
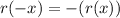
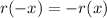
So
 is odd.
is odd.
III
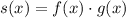
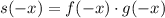
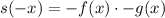
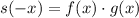
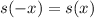
So
 is even.
is even.
So I and II are odd and III is even.
C. is the answer.