Question

Lim 1 - cos 40
x>01 - cos 60​

Answer 1

The answer is 4/9 if the problem is:

`\lim_(\theta \rightarrow 0)(1-\cos(4\theta))/(1-\cos(6\theta))`.

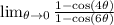Explanation:

I think this says:

`\lim_(\theta \rightarrow 0)(1-\cos(4\theta))/(1-\cos(6\theta))`.

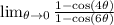Please correct me if I'm wrong about the problem.

Here are some useful limits we might use:

`\lim_(u \rightarrow 0)(\sin(u))/(u)=1`

`\limg_(u \rightarrow 0)(\cos(u)-1)/(u)=0`

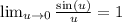
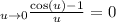
So for our limit... I'm going to multiply top and bottom by the conjugate of the bottom; that is I'm going to multiply top and bottom by
`1+\cos(6\theta)`:

`\lim_(\theta \rightarrow 0)(1-\cos(4\theta))/(1-\cos(6\theta))\cdot(1+\cos(6\theta))/(1+\cos(6\theta))`

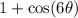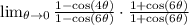
When you multiply conjugates you only have to do first and last of FOIL:

`\lim_(\theta \rightarrow 0)((1-\cos(4\theta))(1+\cos(6\theta)))/(1-\cos^2(6\theta))`

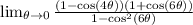
By the Pythagorean Identities, the denominator is equal to
`\sin^2(6\theta)`:

`\lim_(\theta \rightarrow 0)((1-\cos(4\theta))(1+\cos(6\theta)))/(\sin^2(6\theta))`

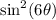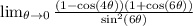
I'm going to divide top and bottom by
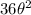`36\theta^2` in hopes to use the useful limits I mentioned:

`\lim_(\theta \rightarrow 0)(((1-\cos(4\theta))(1+\cos(6\theta)))/(36\theta^2))/((\sin^2(6\theta))/(36\theta^2))`

Let's tweak our useful limits I mentioned so it is more clear what I'm going to do in the following steps:

`\lim_(\theta \rightarrow 0)(\sin(6\theta))/(6\theta)=1`

`\lim_(\theta \rightarrow 0)(\cos(4\theta)-1)/(4\theta)=0`

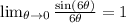
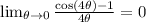
The bottom goes to 1. The limit will go to whatever the top equals if the top limit exists.

So let's look at the top in hopes it goes to a number:

`\lim_(\theta \rightarrow 0)(1-\cos(4\theta))/(36\theta^2) \cdot (1+\cos(6\theta)}`

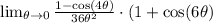
We are going to multiple the first factor by the conjugate of the top; that is we are multiply top and bottom by
`1+\cos(4\theta)`:

`\lim_(\theta \rightarrow 0)(1-\cos(4\theta))/(36\theta^2) \cdot (1+\cos(4\theta))/(1+\cos(4\theta)) \cdot (1+\cos(6\theta)}`

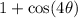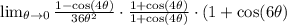
Recall the thing I said about multiplying conjugates:

`\lim_(\theta \rightarrow 0)(1-\cos^2(4\theta))/(36\theta^2) \cdot (1+\cos(6\theta))/(1+\cos(4\theta))`

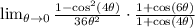
We are going to apply the Pythagorean Identities here:

`\lim_(\theta \rightarrow 0)(\sin^2(4\theta))/(36\theta^2) \cdot (1+\cos(6\theta))/(1+\cos(4\theta))`

`\lim_(\theta \rightarrow 0)(\sin^2(4\theta))/((9)/(4)(4\theta)^2) \cdot (1+\cos(6\theta))/(1+\cos(4\theta))`

`\lim_(\theta \rightarrow 0)(4)/(9)(\sin^2(4\theta))/((4\theta)^2) \cdot (1+\cos(6\theta))/(1+\cos(4\theta))`

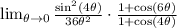
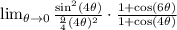
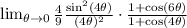
Ok this looks good, we are going to apply the useful limits I mentioned along with substitution to find the remaining limits:

`(4)/(9)(1)^2 (1+\cos(6(0)))/(1+\cos(4(0)))`

`(4)/(9)(1)(1+1)/(1+1)`

`(4)/(9)(1)(2)/(2)`

`(4)/(9)(1)`

`(4)/(9)`

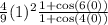
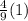
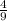
The limit is 4/9.