Question

29) A tank contains 100 gallons of water in which 40 pounds of salt are dissolved. It isdesired to reduce the concentration of salt to 0.1 pounds per gallon by pouring in purewater at the rate of 5 gallons per minute and allowing the mixture (which is kept uniformby stirring) to flow out at the same rate. How long will this take

Answer 1

The amount of salt in the tank at time
`t`, denoted by
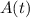`A(t)`, changes over time according to the differential equation,

`(\mathrm dA)/(\mathrm dt)=-\left(\frac A{100}(\rm lb)/(\rm gal)\right)\left(5(\rm gal)/(\rm min)\right)`

`\implies(\mathrm dA)/(\mathrm dt)+\frac A{20}=0`

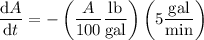
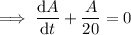
Multiply both sides by
`e^(t/20)`:

`e^(t/20)(\mathrm dA)/(\mathrm dt)+(e^(t/20))/(20)A=0`

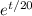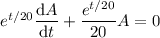
Now the left side can be condensed to the derivative of a product:

`(\mathrm d)/(\mathrm dt)[e^(t/20)A]=0`

Integrate both sides to get

`e^(t/20)A=C`

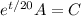
and solving for
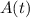`A(t)` gives

`A(t)=Ce^(-t/20)`

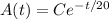
Given that there are 40 pounds of salt at the start, or
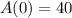`A(0)=40`, we know
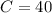`C=40`, so that

`A(t)=40e^(-t/20)`

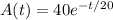
We want the concentration to fall to 0.1 lb/gal, which means

`(40e^(-t/20))/(100)(\rm lb)/(\rm gal)=0.1(\rm lb)/(\rm gal)`

`\implies e^(-t/20)=\frac1{40}`

`\implies-\frac t{20}=-\ln40`

`\implies\boxed{t=20\ln40\approx73.78}`

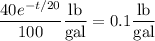
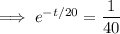
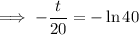
so it would take about 73.78 minutes, or about 1.23 hours, for the concentration to fall to 0.1 lb/gal.